Question

PLEASE HELP (30 POINTS) Solve the rational equation x/3 = x^2/x + 5 , and check for extraneous solutions.

A. x = 0; x = -5/2 is an extraneous solution
B. x = 5/2; x = 0 is an extraneous solution
C. x = 0 and x = 5/2
D. x = 0 and x = -5/2

Answer 1

Option C:
`x=0` and
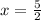`x=(5)/(2)` are the solutions.

Step-by-step explanation:

The equation is
`(x)/(3) =(x^(2) )/(x+5)`

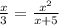
We shall determine the value of x, by simplifying the equation.

`$\begin{aligned} x(x+5) &=3 x^(2) \\ x^(2)+5 x &=3 x^(2) \\ 2 x^(2)-5 x &=0 \\ x(2 x-5) &=0 \end{aligned}$`

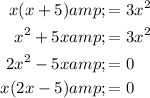
Thus,
`x=0` and
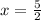`x=(5)/(2)` are the solutions.

Now, let us check whether the solutions are extraneous solutions.

Let us substitute
`x=0` in the original equation to check whether both sides of the equation are equal.

`\begin{aligned}&(0)/(3)=(0^(2))/(0+5)\\&0=(0)/(5)\\&0=0\end{aligned}`

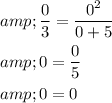
Thus, both sides of the equation are equal.

Hence
`x=0` is a true solution.

Now, Let us substitute
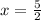`x=(5)/(2)` in the original equation to check whether both sides of the equation are equal.

`\begin{aligned}(\left((5)/(2)\right))/(3) &=(\left((5)/(2)\right)^(2))/(\left((5)/(2)\right)+5) \\(5)/(6) &=(\left((25)/(4)\right))/(\left((15)/(2)\right)) \\(5)/(6) &=(5)/(6)\end{aligned}`

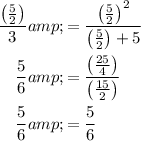
Thus, both sides of the equation are equal.

Hence,
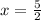`x=(5)/(2)` is a true solution.

Thus, solutions are not extraneous.

Hence, Option C is the correct answer.