Question

A survey of dance club goers found that 35% of club goers prefer trance music, 25% prefer dubstep and 15% preferred both trance and dubstep. What percent of students don't prefer either trance nor dubstep

Answer 1

55% of students don't prefer either trance nor dubstep.

Explanation:

We solve this problem building the Venn's diagram of these probabilities.

I am going to say that:

A is the probability that a club goer prefers trance music.

B is the probability that a club goer prefers dubstep.

C is the probability that a club goer does not like any of these.

We have that:

`A = a + (A \cap B)`

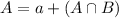
In which a is the probability that a club goer likes trance music and not dubtep and
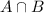`A \cap B` is the probability that a club goer likes both of these styles

By the same logic, we have that:

`B = b + (A \cap B)`

Either a person likes at least one these styles, or they prefer other styles. The sum of these probabilities is decimal 1. So:

`P(A \cup B) + C = 1`

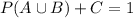
We want to find C to solve this question. So

`C = 1 - P(A \cup B)`

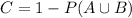
In which

`P(A \cup B) = a + b + (A \cap B)`

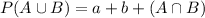
15% preferred both trance and dubstep

This means that
`A \cap B = 0.15`

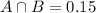
25% prefer dubstep

This means that
`B = 0.25`

`B = b + (A \cap B)`

`0.25 = b + 0.15`

`b = 0.10`

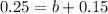
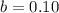
35% of club goers prefer trance music

`A = a + (A \cap B)`

`0.35 = a + 0.15`

`a = 0.20`

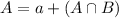
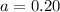
What percent of students don't prefer either trance nor dubstep

`P(A \cup B) = a + b + (A \cap B) = 0.20 + 0.10 + 0.15 = 0.45`

`C = 1 - P(A \cup B) = 1-0.45 = 0.55`

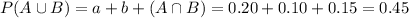
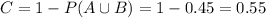
55% of students don't prefer either trance nor dubstep.