Question

Two conducting spheres of different sizes are at the same potential. The radius of the larger sphere is four times larger than that of the smaller sphere. If a total charge Q is placed on this system, what fraction of Q sits on the larger sphere?(Give your answer as a decimal. For example, if the answer is 1/3 then input 0.333.)

Answer 1

0.8

Step-by-step explanation:

The two spheres have the same potential, V.

Let the radius of the larger sphere be R and the radius of the smaller sphere be r,

=> R = 4r

Let the charge on the smaller sphere be q. Hence, the larger sphere will have charge Q - q.

The potential of the smaller sphere will be:

`V_S = (kq)/(r)`

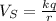
The potential of the larger sphere will be:

`V_L = (k(Q - q))/(R)`

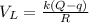
Inputting R = 4r,

`V_L = (k(Q - q))/(4r)`

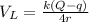
Since
`V_S = V_L = V`,

`(k(Q - q))/(4r) = (kq)/(r)`

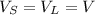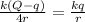
=> Q - q = 4q

=> 5q = Q

q = 0.2Q

The fraction of the charge Q that rests on the smaller sphere is 0.2

The charge of the larger sphere is:

Q - q = Q - 0.2Q = 0.8Q

∴ The fraction of the total charge Q that rests on the larger sphere is 0.8