Area of second figure is 56.6 square meter
Solution:
Given that,
Two given figures are similar
Perimeter of first figure = 20 m
Perimeter of second figure = 34 m
Area of first figure = 19.6 square meter
Area of second figure = ?
Find the ratio of perimeter of first figure to second
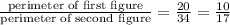
In two similar triangles: The perimeters of the two triangles are in the same ratio as the sides
Therefore,
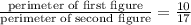
If two figures are similar, then ratio of their perimeters is equal to ratio of their sides
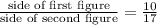
Taking square on both sides, then it becomes ratio of their areas
Because,
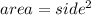
Therefore,

Thus area of second figure is 56.6 square meter