Answer:
Tangential speed=5.4 m/s
Radial acceleration=

Step-by-step explanation:
We are given that
Angular speed=2.59 rev/s
We know that
1 revolution=
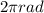
2.59 rev=

By using
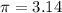
Angular velocity=
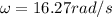
Distance from axis=r=0.329 m
Tangential speed=
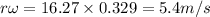
Radial acceleration=
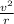
Radial acceleration=
