Question

What is the frequency of blue light with a wavelength of 400 nm?

A. 1.33 × 10³Hz
B. 7.50 × 10¹²Hz
C. 1.33 × 10¹⁴Hz
D. 7.50 × 10¹⁴Hz

Answer 1

`f_(blue)= (3x10^8 m/s)/(4x10^(-7) m)= 7.5 x10^(14) Hz`

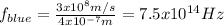
So then our answer would be:

D. 7.50 × 10¹⁴Hz

Step-by-step explanation:

For this case we know the frequency for the blue light, given by the problem:

`\lambda_(blue)= 400 nm`

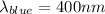
We can convert this into m like this:

`\lambda_(blue)= 400 nm *(10^(-9)m)/(1nm)= 400x10^(-9)m = 4x10^(-7)m`

We know that the speed of light is a constant and is given by:

`v_(light)= 3x10^(8) (m)/(s)`

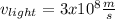
And assuming that we have a fundamental wave, we need to satisfy the following basic relationship:

`v = \lambda f`

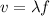
And if we solve for the frequency from the last formula we got:

`f = (v)/(\lambda)`

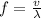
Now if we replace the values given we have:

`f_(blue)= (3x10^8 m/s)/(4x10^(-7) m)= 7.5 x10^(14) Hz`

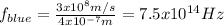
So then our answer would be:

D. 7.50 × 10¹⁴Hz