Answer:
The probability that he makes the free throw in all three attempts is 0.7787.
Explanation:
Let X = number of free throw attempts Steph Curry makes.
The probability that Steph Curry makes a free throw is, p = 0.92.
The number of free throws he gets is, n = 3.
Then the random variable X follows a Binomial distribution with parameters, n = 3 and p = 0.92.
The probability function for binomial is:
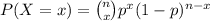
The probability that he makes the free throw in all three attempts is:
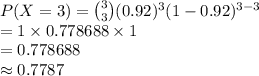
Thus, the probability that he makes the free throw in all three attempts is 0.7787.