Question

A factory is to be built on a lot measuring 210 ft by 280 ft. A local building code specifies that a lawn of uniform width and equal in area to the factory must surround the factory. What must the width of the lawn be and what are the dimensions of the factory?

Answer 1

Width of lawn = 35 ft

Dimensions of factory = length: 210 ft, width: 140 ft

Explanation:

The total area of the lot can be calculated as:

`A_(lot) = 210 * 280\\A_(lot) = 58800 ft^(2)`

Since, the area of factory should be equal to area of lawn:

`A_(lot) = A_(factory) + A_(lawn)\\58800 = 2 A_(factory or lawn)\\\\A_(factory or lawn) = (58800)/(2)\\A_(factory or lawn) = 29400 ft^(2)`

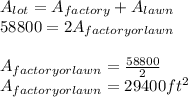
Now, let 'x' be the width of lawn, the dimensions of factory can be written as:

`(210-2x)\\(280-2x)\\`

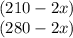
Since, area is equal to length x width:

`(210-2x)*(280-2x) = 29400\\Simplifying:\\210*280 - 210*2x - 2x*280 + 4x^(2) = 29400\\58800 - 420x - 560x +4x^(2) = 29400\\4x^(2) - 980x +58800 = 29400\\4x^(2) - 980x + 29400 = 0\\`

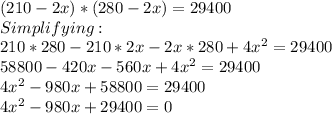
Divide whole equation by 4,

`x^(2) - 245 + 7350 = 0\\`

Solving above quadratic equation, we get,

`x = 210\\x = 35\\`

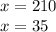
x = 35 seems realistic width of the lawn.

Now, finding the dimension of factory:

`(210-2x) = 210 - 2(35) = 140 ft\\(280-2x) = 280 - 2(35) = 210ft`

We can also reconfirm the area of factory by multiplying the above two lengths:

140 * 210 = 29400 ft