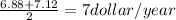Answer with Step-by-step explanation:
We are given that
Initial deposit=$100
Interest rat=r=7%
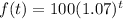 (in dollars)
(in dollars)
Where t(in years)
a.We have to find the rate of change of f(t).
f(t) varies with t Where f(t) in years and t in years
Therefore, the unit of rate of change of f(t) is dollar/year.
b.We have to find the average rate of change over [0,-0.5] and [0,1].
Substitute t=0

Substitute t=0.5

Substitute t=1
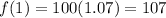
Average rate on interval [a,b] =
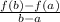
Using the formula
Average rate on interval [0,0.5]=

Average rate on interval [0,0.5]=
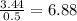 dollar/year
dollar/year
Average rate on interval [0,1]=

c.Average rate on interval [0.5,1]=
 dollars/year
dollars/year
Instantaneous rate of change at t=0.5 =Average of the average values obtained on interval [0,0.5] and [0.5,1]=