Answer:
⠀
Step-by-step explanation :
⠀
As it is given that, the legnth of a rectangle is three times its width and the perimeter is 64 in and we are to find the length and width of the rectangle. So,
⠀
Let us assume the width of the rectangle as w inches and therefore, the length will be 3w inches .
⠀
Now, According to the Question :
⠀

⠀
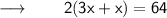
⠀
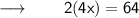
⠀
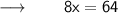
⠀
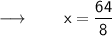
⠀
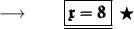
⠀
Therefore,
- The width of the rectangle is 8 inches .
⠀
Now, We are to find the length of the rectangle:
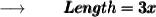
⠀

⠀

⠀
Therefore,
- The length of the rectangle is 24 inches .
⠀