Option B:
The 12th term is 354294.
Solution:
Given data:
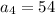 and
and
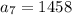
To find
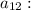
The given sequence is a geometric sequence.
The general term of the geometric sequence is
 .
.
If we have 2 terms of a geometric sequence
 and
and
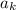 (n > K),
(n > K),
then we can write the general term as
 .
.
Here we have
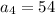 and
and
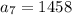 .
.
So, n = 7 and k = 4 ( 7 > 4)
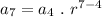

This can be written as
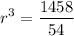
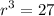
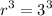
Taking cube root on both sides of the equation, we get
r = 3
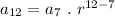


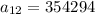
Hence the 12th term of the geometric sequence is 354294.