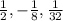Question

The first term of a geometric sequence is -2 and the common ratio is -1/4. what are the next three terms of the sequence?

answer = B

Answer 1

`(1)/(2),-(1)/(8), (1)/(32)`

Explanation:

From the question;

• The first term of a geometric sequence, a₁ is -2
• The common ratio, r is -1/4

We are required to determine the next three terms of the sequence;

We need to know that;

nth term is a geometric sequence is given by;

`T_n=a_1r^n^-^1`

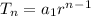
Therefore;

Second term will be given by;

`T_2=-2(-(1)/(4))^2^-^1`

`T_2=-2(-(1)/(4))^1`

`T_2=(1)/(2)`

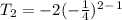
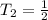
Third term will be given by;

`T_3=-2(-(1)/(4))^3^-^1`

`T_3=-2(-(1)/(4))^2`

`T_3=-2((1)/(16))`

`T_3=1(1)/(8)`

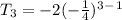
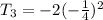
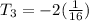
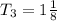
Fourth term will be given by;

`T_4=-2(-(1)/(4))^4^-^1`

`T_4=-2(-(1)/(4))^3`

`T_4=-2(-(1)/(64))\\T_4=(1)/(32)`

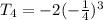
Thus, the next three terms are;
`(1)/(2),-(1)/(8), (1)/(32)`