Answer:
The given expression is equal to 25.
Explanation:
The given expression is
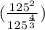
To simplify this expression, we have to divide powers, which implies to subtract exponenets, as follows
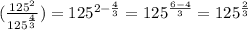
Then, we use the exponent property to transform the obtained power to a root
![125^{(2)/(3) }=\sqrt[3]{125^(2) } =\sqrt[3]{15625} =25](https://img.qammunity.org/2021/formulas/mathematics/middle-school/mrov09u0y5gaj39p6ztly2dcpvqvzwpuxr.png)
Therefore, the given expression is equal to 25.