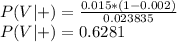Question

Suppose a test for a virus has a false-positive rate of 0.009 and a false-negative rate of 0.002. Assume that 1.5% of the population has the virus. (a) What is the chance someone from this population will test positive? (Enter exact answer.) (b) If someone tests positive, what is the chance he actually has the virus? (Answer correct to four decimal places.)

Answer 1

(a) 0.023835

(b) 0.6281

Explanation:

(a) The chance someone from this population will test positive is given by the percentage of people who have the virus multiplied by the change of testing positive (1 - false-negative rate) added to the percentage of people who do not have the virus multiplied by the change of testing positive (false-positive rate)

`P(+) = 0.015*(1-0.002)+(1-0.015)*0.009\\P(+) = 0.023835`

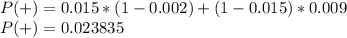
(b) The probability that someone actually has the virus given that they have tested positive is determined as the probability of having the virus and testing positive divided by the probability of testing positive:

`P(V|+) = ( 0.015*(1-0.002))/(0.023835)\\P(V|+) = 0.6281`