Question

Compute the ratio of the rate of heat loss through a single-pane window with area 0.15 m2 to that for a double-pane window with the same area. The glass of a single pane is 4.5 mm thick, and the air space between the two panes of the double-pane window is 6.60 mm thick. The glass has thermal conductivity 0.80 W/m⋅K. The air films on the room and outdoor surfaces of either window have a combined thermal resistance of 0.15 m2⋅K/W. Express your answer using two significant figures.

Answer 1

2.80321285141

Step-by-step explanation:

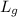`L_g` = Thickness of glass = 4.5 mm

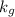`k_g` = Thermal conductivity of glass = 0.8 W/mK

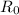`R_0` = Combined thermal resistance =
`0.15* m^2K/W`

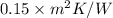
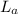`L_a` = Thickness of air = 6.6 mm

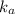`k_a` = Thermal conductivity of air = 0.024 W/mK

The required ratio is the inverse of total thermal resistance

`(2(L_g/k_g)+R_0+(L_a/k_a))/((L_g/k_g)+R_0)\\ =(2(4.5* 10^(-3)/0.8)+0.15+(6.6* 10^(-3)/0.024))/((4.5* 10^(-3)/0.8)+0.15)\\ =2.80321285141`

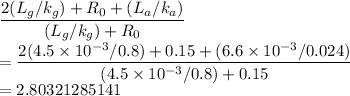
The ratio is 2.80321285141

Answer 2

`(\dot Q)/(\dot Q') =2.6668`

Step-by-step explanation:

Given:

• area of the each window panes,
  `A=0.15\ m^2`

• thickness of each pane,
  `t_g=4.5* 10^(-3)\ m`

• air gap between the two pane of a double pane window,
  `t_a=6.6* 10^(-3)\ m`

• thermal conductivity of glass,
  `k_g=0.8\ W.m^(-1).K^(-1)`

• thermal resistance of the air on the either sides of double pane window,
  `R_(th)=0.15\ m^2.K.W^(-1)`

Heat loss through single pane window:

Using Fourier's law of conduction,

`\dot Q=A.dT/ (R_(th)+(t_g)/(k) )`

`\dot Q=0.15* dT/ (0.15+(4.5* 10^(-3))/(0.8))`

`\dot Q=0.9638\ dT\ [W]`

Heat loss through double pane window:

`\dot Q'=dT* A/(R_(th)+2* (t_g)/(k)+(t_a)/(k_a) )`

where:

`dT=` change in temperature

`k_a=` coefficient of thermal conductivity of air
`= 0.026\ W.m^(-1).K^(-1)`

`\dot Q'=dT* 0.15/ (0.15+2* (4.5* 10^(-3))/(0.8)+(6.6* 10^(-3))/(0.026))`

`\dot Q'=0.3614\ dT\ [W]`

Now the ratio:

`(\dot Q)/(\dot Q') =(0.9638(dT))/(0.3614(dT))`

`(\dot Q)/(\dot Q') =2.6668`