Question

What is the orthocenter of a triangle on (-2,5), (6,5), and (4,-1)

Answer 1

(4,3)

Explanation:

The orthocenter of a triangle is the point of intersection of the altitudes of the triangle .

The vertices are:

A(-2,5), B(6,5), and C(4,-1)

Slope of (6,5), and (4,-1) is

`m = (5 - - 1)/(6 - 4) = 3`

Slope of altitude through A is

`- (1)/(3)`

The equation of the altitude through A is

`y - 5 = - (1)/(3) (x - - 2)`

`y = - (1)/(3) x + (13)/(3)`

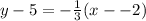
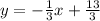
The slope of A(-2,5), B(6,5) is zero because it is a horizontal line.

The equation of altitude through (4,-1) will be the vertical line x=4.

This implies that,

`y = - (4)/(3) + (13)/(3) = 3`

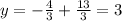
Hence the orthocenter is (4,3)