Question

A lab technician is tested for her consistency by making multiple measurements of the cholesterol level in one blood sample. The target precision is a standard deviation of or less. If 20 measurements are taken and the standard deviation is is there enough evidence to support the claim that her standard deviation is greater than the target, at

Answer 1

`\chi^2 =(20-1)/(1) 4.84 =91.96`

`p_v =P(\chi^2 >91.96) \approx 0`

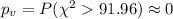
"=1-CHISQ.DIST(91.96,19,TRUE)"

If we compare the p value and the significance level provided we see that
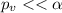`p_v <<\alpha` so on this case we have enough evidence in order to reject the null hypothesis at the significance level provided. And we have evidence to conclude that the sample variance is higher than 1 and indeed that the deviation is higher than 1 mg/dL

Explanation:

Assuming this problem:"A lab technician is tested for her consistency by making multiple measurements of the cholesterol level in one blood sample. The target precision is a standard deviation of 1 mg/dL or less. If 20 measurements are taken and the standard deviation is 2.2 mg/dL, is there enough evidence to support the claim that her standard deviation is greater than the target, at a significance level of= .01? "

Notation and previous concepts

A chi-square test is "used to test if the variance of a population is equal to a specified value. This test can be either a two-sided test or a one-sided test. The two-sided version tests against the alternative that the true variance is either less than or greater than the specified value"

`n=20` represent the sample size

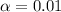`\alpha=0.01` represent the confidence level

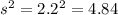`s^2 =2.2^2 =4.84` represent the sample variance obtained

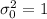`\sigma^2_0 =1` represent the value that we want to test

Null and alternative hypothesis

On this case we want to check if the population variance specification is violated, so the system of hypothesis would be:

Null Hypothesis:
`\sigma^2 \leq 1`

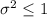
Alternative hypothesis:
`\sigma^2 >1`

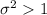
Calculate the statistic

For this test we can use the following statistic:

`\chi^2 =(n-1)/(\sigma^2_0) s^2`

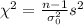
And this statistic is distributed chi square with n-1 degrees of freedom. We have eveything to replace.

`\chi^2 =(20-1)/(1) 4.84 =91.96`

Calculate the p value

In order to calculate the p value we need to have in count the degrees of freedom , on this case 20-1=19. And since is a right tailed test the p value would be given by:

`p_v =P(\chi^2 >91.96) \approx 0`

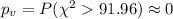
In order to find the p value we can use the following code in excel:

"=1-CHISQ.DIST(91.96,19,TRUE)"

Conclusion

If we compare the p value and the significance level provided we see that
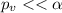`p_v <<\alpha` so on this case we have enough evidence in order to reject the null hypothesis at the significance level provided. And we have evidence to conclude that the sample variance is higher than 1 and indeed that the deviation is higher than 1 mg/dL