Question

An elementary school is offering 2 language classes: one in Spanish (S) and one in French (F). Given that P(S) = 50%, P(F) = 40%, P(S ∪ F) = 70%, find the probability that a randomly selected student (a) is taking Spanish given that he or she is taking French; (b) is not taking French given that he or she is not taking Spanish. 2. A pair of fair dice is rolled until a sum of either 5 or 7 appears.

Answer 1

(a) Probability that a randomly selected student is taking Spanish given that he or she is taking French = 0.5 .

(b) Probability that a randomly selected student is not taking French given that he or she is not taking Spanish = 0.6 .

Explanation:

We are given that an elementary school is offering 2 language classes ;

Spanish Language is denoted by S and French language is denoted by F.

Also we are given, P(S) = 0.5 {Probability of students taking Spanish language}

P(F) = 0.4 {Probability of students taking French language}

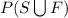`P(S\bigcup F)` = 0.7 {Probability of students taking Spanish or French Language}

We know that,
`P(A\bigcup B)` =
`P(A) + P(B) -`
`P(A\bigcap B)`

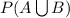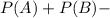
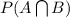
So,
`P(S\bigcap F)` =
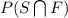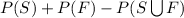`P(S) + P(F) - P(S\bigcup F)` = 0.5 + 0.4 - 0.7 = 0.2

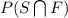`P(S\bigcap F)` means Probability of students taking both Spanish and French Language.

Also, P(S)' = 1 - P(S) = 1 - 0.5 = 0.5

P(F)' = 1 - P(F) = 1 - 0.4 = 0.6

`P(S'\bigcap F')` = 1 -
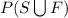`P(S\bigcup F)` = 1 - 0.7 = 0.3

(a) Probability that a randomly selected student is taking Spanish given that he or she is taking French is given by P(S/F);

P(S/F) =
`(P(S\bigcap F))/(P(F))` =
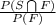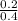`(0.2)/(0.4)` = 0.5

(b) Probability that a randomly selected student is not taking French given that he or she is not taking Spanish is given by P(F'/S');

P(F'/S') =
`(P(S'\bigcap F'))/(P(S'))` =
`(1- P(S\bigcup F))/(1-P(S))` =
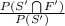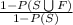`(0.3)/(0.5)` = 0.6 .

Note: 2. A pair of fair dice is rolled until a sum of either 5 or 7 appears ; This question is incomplete please provide with complete detail.