Question

The plates of a parallel-plate capacitor have constant charges of +Q and?Q. Do the following quantities increase, decrease, or remain the same as the separation of the plates is increased?

A) the electric field between the plates
B) the potential difference between the plates
C) the capacitance
D) the energy stored in the capacitor

Answer 1

a)constant

b)constant

c)constant

d) constant

Step-by-step explanation:

a)

The electric field between the plates remain constant. The Electric field between the plates is given as:

`E=(\sigma)/(\epsilon)`

where:

`\sigma=` surface charge density

`\epsilon=` permittivity of the material between the plates

b)

The potential difference between the plates is related as:

`V=(Q)/(C)`

and

`E=(V)/(d)`

where:

d = distance between the plates

Therefore the potential difference remains constant when the capacitor plates distance remains constant.

c)

the capacitance:

`C=(Q)/(V)`

When the charge and potential difference is constant then the capacitance also remains constant.

d)

Energy stored in a capacitor:

`U=(1)/(2) C.V^2`

Since capacitance and potential difference are constant therefore potential difference is also constant.

Answer 2

Step-by-step explanation:

(A) Electric field for the parallel plate capacitor is given by :

`E=(\sigma)/(2\epsilon_o)`

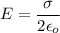
It is clear that the electric field does not depend on the separation of the plates.

(B) The relation between the electric field and the electric potential is given by :

`V=Ed`

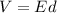
d is the separation between plates. So, if the separation of the plates is increased, the potential difference increases.

(C) The capacitance of the parallel plate capacitor is given by :

`C=(A\epsilon_o)/(d)`

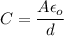
So, the capacitance decreases when the separation of the plates is increased.

(D) The energy stored in the capacitor is given by :

`E=(1)/(2)CV^2`

`E=(1)/(2)C(Ed)^2`

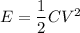
So, the energy stored in the capacitor is increased when the separation of the plates is increased.