Question

a large parallel plate capacitor has plate seperation of 1.00 cm and plate area of 314 cm^2. The capacitor is connected across a voltage of 20.0 V and has air betweeen the plates. How much work is done on the capacitor as the plate seperation is inceased to 2.00 cm?

Answer 1

`W = -2.76* 10^(-9)~J`

Step-by-step explanation:

The work done on the capacitor is equal to the difference in potential energy stored in the capacitor in two different cases.

The potential energy is given by the following formula:

`U = (1)/(2)CV^2`

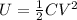
where C can be calculated using the plate separation and area.

`C = \epsilon(A)/(d) = \epsilon(0.0314)/(0.01) = 3.14\epsilon`

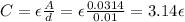
Therefore, the potential energy in the first case is

`U = (1)/(2)3.14\epsilon (20)^2 = 628\epsilon`

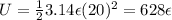
In the second case:

`C_2 = \epsilon(A)/(d) = \epsilon(0.0314)/(0.02) = 1.57\epsilon\\U = (1)/(2)C_2 V^2 = (1)/(2)1.57\epsilon (20)^2 = 314\epsilon`

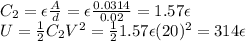
The permittivity of the air is very close to that of vacuum, which is 8.8 x 10^-12.

So, the difference in the potential energy is

`W = U_2 - U_1 = \epsilon(314 - 628) = -314 * 8.8 * 10^(-12) = -2.76* 10^(-9)~J`