Question

A loaded grocery cart is rolling across a parking lot in a strong wind. You apply a constant force \vec{F} =(33 N)\hat{i} - (41 N)\hat{j} to the cart as it undergoes a displacement \vec{s} = (-9.4 m)\hat{i} - (3.1 m)\hat{j}.

Part A
How much work does the force you apply do on the grocery cart?
Express your answer using two significant figures.
W =

{\rm J}

Answer 1

-180 J

Step-by-step explanation:

We are given that

Constant force=
`F=(33 N)\hat{i}-(41 N)\hat{j}`

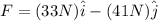
Displacement=
`\vec{s}=(-9.4m)\hat{i}-(3.1m)\hat{j}`

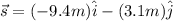
We have to find the work done .

We know that

Work done=
`F\cdot s`

Using the formula

Work done=
`(33i-41j)\cdot (-9.4i-3.1j)`

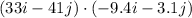
Work done =
`33i\cdot (-9.4)i+41j\cdot 3.1 j`

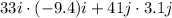
By using rule
`i\cdot i=j\cdot j=k\cdot k=1,i\cdot j=j\cdot k=k\cdot i=i\cdot k=k\cdot j=j\cdot i=0`

Work done=
`-310.2+127.1`

Work done=-183.1 J

We have to write answer in two significant figures.

When units digit 3 is less than 5 then digits on left side of 3 remains same and digits on right side of 3 and 3 will be replace by zero

Work done=-180 J

Hence, the work done =-180 J

Answer 2

`W=-183.1\ J`

Step-by-step explanation:

Given:

force applied,
`\vec{F} =(33 N)\hat{i} - (41 N)\hat{j}`

displacement caused,
`\vec{s} = (-9.4 m)\hat{i} - (3.1 m)\hat{j}`

Work done by the force on the cart:

`W=\vec F.\vec s`

`W=[(33 N)\hat{i} - (41 N)\hat{j}].[(-9.4 m)\hat{i} - (3.1 m)\hat{j}]`

`W=-310.2+127.1`

`W=-183.1\ J`

Negative work means that the force and displacement have an obtuse angle between them.