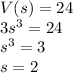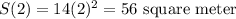Answer:
a)
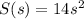
b)
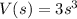
c)
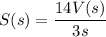
d) 56 square meter
Explanation:
We are given the following in the question:
A closed box with a square bottom is three times high as it is wide.
Let s be the side of square and h be the height.
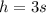
a) Surface area of box
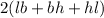
where l is the length, b is the breadth and h is the height.
Putting values:
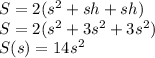
b) Volume of box
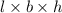
where l is the length, b is the breadth and h is the height.
Putting values:
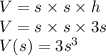
c) Surface area in terms of volume
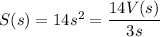
d) Surface area
Volume = 24 m³