Answer:
(12,10)
Explanation:
Let the midpoint of the side opposite this vertex have coordinates B(a,b)
We have the centroid at C(8,7) and the vertex of the triangle at A(0,1).
The centroid divides AB internally in the ratio 2:1
We use the formula:

where m:n=2:1 is the ratio of internal division.
We substitute the coordinates of A and B and the ratio to get:
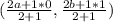
This should simplify and give us the centroid.
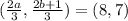
This implies that:
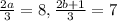
We solve for a and b

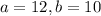
Therefore the midpoint of the side opposite this vertex is (12,10)