Answer:
b) twice the energy of each photon of the red light.
Step-by-step explanation:
Given:
wavelength of red light,

wavelength of ultraviolet light,
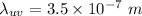
We know that the energy of a photon is given as:
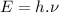 ..............(1)
..............(1)
where:
h = plank's constant
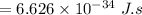
 frequency of the wave
frequency of the wave
we have the relation:
 ...................(2)
...................(2)
From (1) and (2) we have:
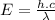
Energy of photons for ultraviolet light:
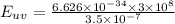
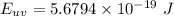
Since the energy of photons is inversely proportional to the wavelength of the light hence the photon-energy of ultraviolet light is double of the photon-energy of the red light as the wavelength of the red light is twice to that of ultraviolet light.