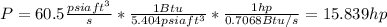Question

A water pump increases the water pressure from 15 psia to 70 psia. Determine the power input required, in hp, to pump 1.1 ft3/s of water. Does the water temperature at the inlet have any significant effect on the required flow power?

Answer 1

`P= 60.5 (psia ft^3)/(s) *(1 Btu)/(5.404 psia ft^3) *(1 hp)/(0.7068 Btu/s)= 15.839 hp`

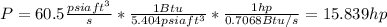
Step-by-step explanation:

Notation

For this case we have the following pressures:

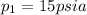`p_1 = 15 psia` initial pressure

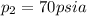`p_2 = 70 psia` final pressure

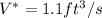`V^(*) = 1.1 ft^3/s` represent the volumetric flow

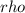`rho` represent the density

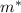`m^(*)` represent the mass flow

Solution to the problem

From the definition of mass flow we have the following formula:

`m^(*) = \rho V^(*)`

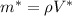
For this case we can calculate the total change is the sytem like this:

`\Delta E= (p_2 -p_1)/(\rho)`

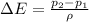
Since we just have a change of pressure and we assume that all the other energies are constant.

The power is defined as:

`P = m^* \Delta E`

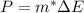
And replacing the formula for the change of energy we got:

`P = m V^* (p_2 -p_1)/(\rho) = V^* (p_2 -p_1)`

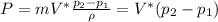
And replacing we have this:

`P= (70-15) psia * 1.1 (ft^3)/(s) =60.5 (psia ft^3)/(s)`

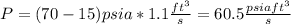
And we can convert this into horsepower like this:

`P= 60.5 (psia ft^3)/(s) *(1 Btu)/(5.404 psia ft^3) *(1 hp)/(0.7068 Btu/s)= 15.839 hp`