Question

The length of a rectangle is five times its width. If the area of the rectangle is 320m, find the perimeter

Answer 1

Answer: The perimeter is 96 m

Explanation:

If we tag the length of the rectangle as
`l` and the width as
`w`, and if in addition we are told
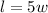`l=5 w`,the dimensions of the rectangle are as shown in the figure.

Now, the area of a rectangle is given by:

`A=(l)(w)=320 m^(2)`

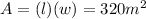
Since
`l=5 w`:

`A=(5w)(w)=320 m^(2)`

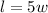Isolating
`w`:

`5w^(2)=320 m^(2)`

`w=\sqrt{(320 m^(2))/(5)}`

`w=8 m`

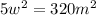
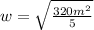
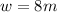
On the other hand, the perimeter of a triangle is given by the addition of each of its sides. Then, if the rectangle has two sides that measure
`w` and two sides that measure
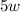`5 w`, the perimeter is:

`P=2(5)(w)+2w`

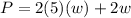
Substituting the value of
`w` in the last equation:

`P=2(5)(8 m)+2(8 m)`

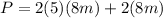
Finally the perimeter is:

`P=96 m`