Answer:
A = $8406.6
Explanation:
Given:
Average rate
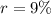
Initial cost of painting

Time
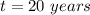
We need to find the final amount of painting at the end of a 20-year.
Solution:
Using Exponential Growth rate formula as:
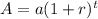 ----------(1)
----------(1)
Where:
A = Final amount
a = Initial amount.
r = Rate as a decimal.
t = Time.
Now, we substitute all given values in equation 1.
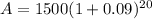
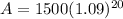
Substitute
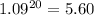 in above equation.
in above equation.
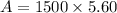
A = $8406.62
Therefore, value of the painting at the end of a 20-year A = $8406.6