Question

This problem involves two distinct sets of events, which we label A1and A2 and B1 and B2. The events A1and A2 are mutually exclusive and collectively exhaustive within their set. The events B1and B2 are mutually exclusive and collectively exhaustive within their set. Intersections can occur between all events from the two sets.Given P(A1)= 0.8, P(B1|A1) = 0.6, and P(B1|A2) = 0.2, what is P(A1|B1)?

Answer 1

0.42

Explanation:

Let the events be given as:

For twp mutually exclusive events, the probability of A1 is given as follows:

P (B1A1) =
`( P(B1) x P (BA1))/(P(A1))`

= 0.6

Solving the equation above to get B1:

P (B1) =
`((0.8)x (0.6))/((0.6))`

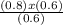
= 0.8

Therefore, computing P (A1B1) gives P(A1) × P (B1)

= (0.8) × (0.6)

= 0.42 Ans