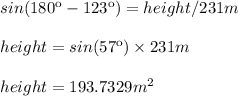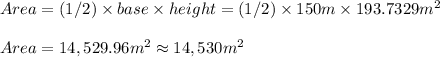Question

Helpppp pleaseeeeeeeeeeeeeee

Answer 1

Find below the calculations of the two areas, each with two methods. The results are:

• Upper triangle:

`Area=5000√(3)units^2`

• Lower triangle:

`Area=14,530m^2`

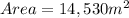
Step-by-step explanation:

A) Method 1

When you are not given the height, but you are given two sides and the included angle between the two sides, you can use this formula:

`Area=side_1* side_2* sin(\alpha)`

Where,
`\alpha` is the measure of the included angle.

1. Upper triangle:

`side_1=200units\\ \\ side_2=100units\\ \\ \alpha =60\º\\ \\ Area=200units* 100units* sin(60\º)/2\\ \\ Area=5000√(3)units^2`

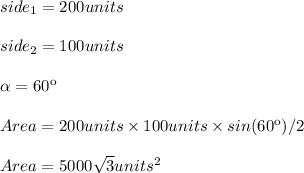
2. Lower triangle:

`side_1=231m\\ \\ side_2=150m\\ \\ \alpha =123\º\\ \\ Area=231m* 150m* sin(123\º)/2\\ \\ Area=14,529.96m^2\approx14,530m^2`

B) Method 2

You can find the height of the triangle using trigonometric properties, and then use the very well known formula:

`Area=(1/2)* base* height`

Use it for both triangles.

3. Upper triangle:

The trigonometric ratio that you can use is:

`sine(\alpha)=opposite\text{ }leg/hypotenuse`

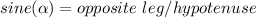
Notice the height is the opposite leg to the angle of 60º, and the side that measures 100 units is the hypotenuse of that right triangle. Then:

`sin(60\º)=height/100units\\ \\ height=sin(60\º)*100units\\ \\ height=50√(3)units`

`Area=(1/2)* base* height=(1/2)* 200units* 50√(3)units=5,000√(3)units^2`

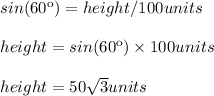
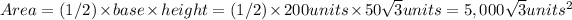
3. Lower triangle:

`sin(180\º-123\º)=height/231m\\ \\ height=sin(57\º)* 231m\\ \\ height=193.7329m^2`

`Area=(1/2)* base* height=(1/2)* 150m* 193.7329m^2\\\\ Area=14,529.96m^2\approx 14,530m^2`