Question

In a recent poll^1 of 1000 American adults, the number saying that exercise is an important part of daily life was 753. Use strategy or other technology to find a 90% confidence interval for the proportion of American adults who think exercise is an important part of daily life. The 90% confidence interval is

Answer 1

`0.753 - 1.64\sqrt{(0.753(1-0.753))/(1000)}=0.731`

`0.753 + 1.64\sqrt{(0.753(1-0.753))/(1000)}=0.775`

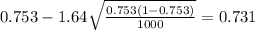
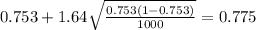
The 95% confidence interval would be given by (0.731;0.775)

Explanation:

Previous concepts

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The population proportion have the following distribution

`p \sim N(p,\sqrt{(p(1-p))/(n)})`

Solution to the problem

In order to find the critical value we need to take in count that we are finding the interval for a proportion, so on this case we need to use the z distribution. Since our interval is at 90% of confidence, our significance level would be given by
`\alpha=1-0.90=0.1` and
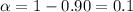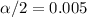`\alpha/2 =0.005`. And the critical value would be given by:

`z_(\alpha/2)=-1.64, z_(1-\alpha/2)=1.64`

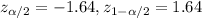
The confidence interval for the mean is given by the following formula:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}`

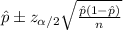
The estimated proportion for this case is:

`\hat p = (X)/(n)= (753)/(1000)=0.753`

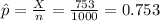
If we replace the values obtained we got:

`0.753 - 1.64\sqrt{(0.753(1-0.753))/(1000)}=0.731`

`0.753 + 1.64\sqrt{(0.753(1-0.753))/(1000)}=0.775`

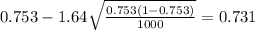
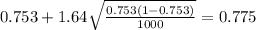
The 95% confidence interval would be given by (0.731;0.775)