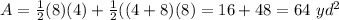Question

Look at the image please helppp

Answer 1

Option A. one rectangle and two triangles

Option E. one triangle and one trapezoid

Explanation:

step 1

we know that

The area of the polygon can be decomposed into one rectangle and two triangles

see the attached figure N 1

therefore

Te area of the composite figure is equal to the area of one rectangle plus the area of two triangles

so

`A=(8)(4)+2[(1)/(2)((8)(4)]=32+32=64\ yd^2`

step 2

we know that

The area of the polygon can be decomposed into one triangle and one trapezoid

see the attached figure N 2

therefore

Te area of the composite figure is equal to the area of one triangle plus the area of one trapezoid

so

`A=(1)/(2)(8)(4)+(1)/(2)((4+8)(8)=16+48=64\ yd^2`