Answer:
Case a Case b
margin of error 0.0216 0.0231
Interval estimate (0.7016 , 0.6795) (0.5031 , 0.4569)
margin of error is not same in both cases.
Explanation:
a
At 95% confidence interval the interval estimate of number of 20 year old drivers in year A can be computed as
p' ± z
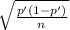
= 0.68 ± 1.96

= 0.7016 , 0.6795
the margin of error can be written as
z
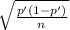
= 1.96

= 0.0216
b
At 95% confidence interval the interval estimate of number of 20 year old drivers in year B can be computed as
p' ± z
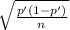
= 0.48 ± 1.96
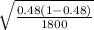
= 0.5031 , 0.4569
the margin of error can be written as
z
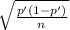
= 1.96
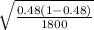
= 0.0231
c
Sample size is same in case A and B but proportion is different in both cases so margin of error is different in both cases