Answer:
62.8 degree
Step-by-step explanation:
Let the incident ray incident at an angle
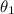 at air glass surface.
at air glass surface.
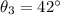 =Angle of refraction when ray travel from glass to water
=Angle of refraction when ray travel from glass to water
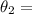 Angle of refraction when the ray travel from air to glass
Angle of refraction when the ray travel from air to glass
Refractive index of glass,

We know that
Refractive index of water=
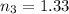
Snell's law
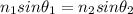
Where
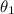 =Angle of incidence
=Angle of incidence
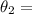 Angle of refraction
Angle of refraction
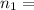 Refractive index of medium 1
Refractive index of medium 1
 Refractive index of medium 2
Refractive index of medium 2
When the ray travel from glass to water
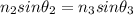
Where
 Refractive index of medium 1(Glass)
Refractive index of medium 1(Glass)
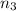 =Refractive index of medium 2 (Water)
=Refractive index of medium 2 (Water)
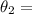 Angle of incidence
Angle of incidence
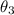 =Angle of refraction
=Angle of refraction
Substitute the values
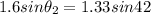
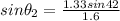
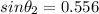
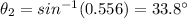
Angle of refraction when ray travel from air to glass= Angle of incidence of when ray travel from glass to water
Angle of refraction when the ray travel from air to glass=33.8 degree
Refractive index of air=
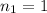
Again apply Snell's law

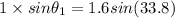
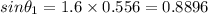
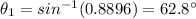
Hence, the angle of the incident ray at the air-glass interface=62.8 degree