Answer:
(a) Probability that a package is delivered by UPS if it weighs 2 lbs or more = 0.0316.
(b) Probability that a package is not delivered by UPS if it weighs 2 lbs or more = 0.9684 .
Explanation:
We are given that 20% of all packages from Amazon are delivered by UPS, from which 12% of the packages that are delivered by UPS weighs 2 lbs or more and 8% of the packages that are not delivered by UPS weighs less than 2 lbs.
Firstly Let A = Package from Amazon is delivered by UPS.
B = Packages that are delivered by UPS weighs 2 lbs or more.
So, P(A) = 0.2 and P(A') = {Probability that package is not delivered by UPS}
P(A') = 1 - 0.2 = 0.8
P(B/A) = 0.12 {means Probability that package weight 2 lbs or more given it
is delivered by UPS}
P(B'/A') = 0.08 [means Probability that package weight less than 2 lbs given
it is not delivered by UPS}
Since, P(B/A) =
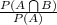 ,
,
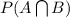 = P(B/A) * P(A) = 0.12 * 0.2 = 0.024 .
= P(B/A) * P(A) = 0.12 * 0.2 = 0.024 .
Also P(B) { Probability that package weight 2 lbs or more} is given by;
- Probability that package weight 2 lbs or more and it delivered by UPS.
- Probability that package weight 2 lbs or more and is not delivered by UPS.
So, P(B) =
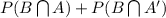 = P(B/A) * P(A) + P(B/A') * P(A')
= P(B/A) * P(A) + P(B/A') * P(A')
= 0.12 * 0.2 + 0.92 * 0.8 { Here P(B/A') = 1 - P(B'/A') = 1 - 0.08 = 0.92}
= 0.76
(a) Probability that a package is delivered by UPS if it weighs 2 lbs or more is given by P(A/B);
P(A/B) =
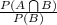 =
=
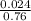 = 0.0316
= 0.0316
(b) Probability that a package is not delivered by UPS if it weighs 2 lbs or more = 1 - P(A/B) = 1 - 0.0316 = 0.9684 .