The value of h(t) when
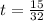 is 10.02.
is 10.02.
Solution:
Given function
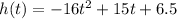
To find the value of h(t) when
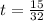 :
:
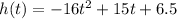
Substitute
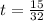 in the given function.
in the given function.
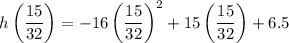
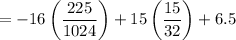
Now multiply the common terms into inside the bracket.
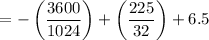
Now, in the first term, the numerator and denominator both have common factor 16. So reduce the first term into the lowest term.
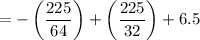
To make the denominator same, take LCM of the denominators.
LCM of 64 and 32 = 64
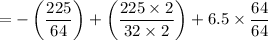
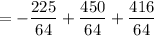
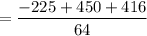
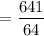
= 10.02
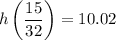
Hence the value of h(t) when
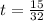 is 10.02.
is 10.02.