Question

For abc shown with vertices at A(-2,6),B(8,-2) and C(-8,-4), shown using coordinate geometry that the segment connecting the midpoint of sides Ac and BC is half the length of side AB.

Answer 1

It is proved that AB = 2 × DE.

Explanation:

The three vertices of triangle ABC are A(-2,6), B(8,-2) and C(-8,-4).

So, the mid point of AC (say D) has coordinates
`((- 2 - 8)/(2),(6 - 4)/(2)) = (-5,1)`.

And the mid point of BC (say E) has coordinates
`((8 - 8)/(2), (- 2 - 4)/(2)) = (0, - 3)`.

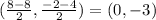Now, the length of DE will be
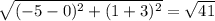`\sqrt{(- 5 - 0)^(2) + (1 + 3)^(2)} = √(41)` units.

Again, the length of AB will be
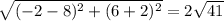`\sqrt{(- 2 - 8)^(2) + (6 + 2)^(2)} = 2√(41)` units.

So, it is proved that AB = 2 × DE. (Answer)