Midpoint of AC = (–1, –1)
Solution:
In the given graph we can find the coordinates of A and C.
Coordinates of A = (–4, 2)
Coordinates of C = (2, –4)
Here,
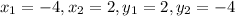
Let us find the midpoint of the segment AC.
Midpoint formula:
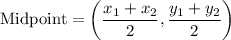
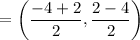
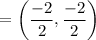
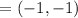
Midpoint of AC = (–1, –1)
Option D is the correct answer.
Hence the coordinates of the midpoint of the line segment AC is (–1, –1).