Answer:
a)
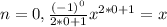
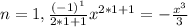
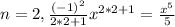
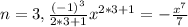
b) n=0
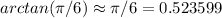
The real value for the expression is
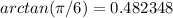
And if we replace into the formula of relative error we got:
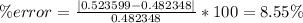
n =1
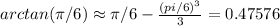
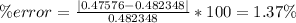
n =2
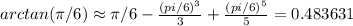
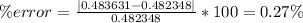
n =3
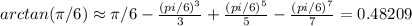
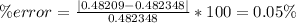
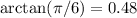
Explanation:
Part a
the general term is given by:
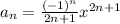
And if we replace n=0,1,2,3 we have the first four terms like this:
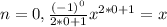
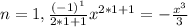
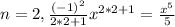
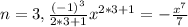
Part b
If we use the approximation
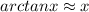 we got:
we got:
n=0
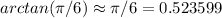
The real value for the expression is
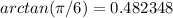
And if we replace into the formula of relative error we got:
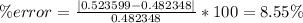
If we add the terms for each value of n and we calculate the error we see this:
n =1
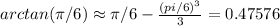
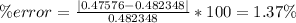
n =2
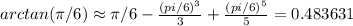
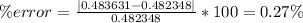
n =3
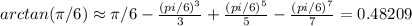
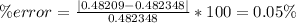
And thn we can conclude that the approximation is given by:
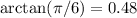
Rounded to 2 significant figures