Answer:
The Final answer will be
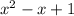 with remainder 0.
with remainder 0.
Explanation:
We have attached the division for your reference.
Given:
Dividend =
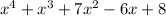
Divisor =
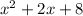
Explaining the division we get;
Step 1: First when we divide the Dividend
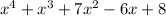 with divisor
with divisor
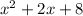 we will first multiply
we will first multiply
 with the divisor then we get the Quotient as
with the divisor then we get the Quotient as
 and Remainder as
and Remainder as
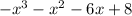
Step 2: Now the Dividend is
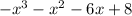 and Divisor
and Divisor
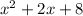 is we will now multiply
is we will now multiply
 with the divisor then we get the Quotient as
with the divisor then we get the Quotient as
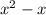 and Remainder as
and Remainder as
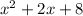
Step 3: Now the Dividend is
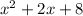 and Divisor is
and Divisor is
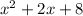 we will now multiply 1 with the divisor then we get the Quotient as
we will now multiply 1 with the divisor then we get the Quotient as
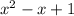 and Remainder as 0.
and Remainder as 0.
Hence The Final answer will be
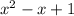 with remainder 0.
with remainder 0.