Answer:

Explanation:
The
 term of an arithmetic sequence is given by:
term of an arithmetic sequence is given by:
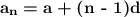
where a is the first term of the sequence
and d is the common difference.
We are given the
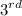 and the
and the
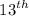 term of the sequence.
term of the sequence.
We are asked to find the
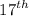 term.
term.
From the formula, we can write
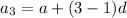
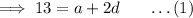
Also,
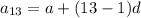
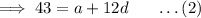
Now, we solve Equation (1) and (2) for a and d.
Solving we get:
a = 7; d = 3
Therefore,
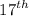 term,
term,
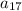 can now be calculated.
can now be calculated.
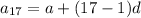
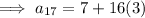
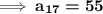
Therefore, the
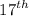 term of the sequence is 55.
term of the sequence is 55.
Hence, the answer.