Answer:
- Using model A, the price should be $ 5 to maximize monthly revenue because the x-intercepts occur at x= 8 and x = -2.
- Using model B, the price should be $ 6 to maximimze monthly revenue because the x-intercepts occur at x = 10 and x = -2.
Step-by-step explanation:
The maximization of the monthly revenue is given by the maximum value of the function, f(x) for the model A and the curve for the model B.
1. Model A.
The function
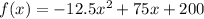 is a quadratic function, a parabola, whose vertex is the maximum value (since the coefficient of the quadratic term is negative, - 2).
is a quadratic function, a parabola, whose vertex is the maximum value (since the coefficient of the quadratic term is negative, - 2).
Then, by finding the x-coordinate ot the vertex you will have the value of x (he number of $1-price increases form the original $ per bottle price) at which such maximum is reached.
To find the vertex you can transform the given function into its vertex form, which is done by completing squares:
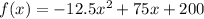
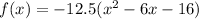

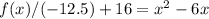

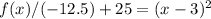
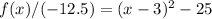
![f(x)=-12.5[(x-3)^2-25]](https://img.qammunity.org/2021/formulas/mathematics/high-school/d1tz3wduqhaobe6ahdsqzy6u51naq776uc.png)
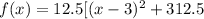
Compare with the general equation of the vertex form for a parabola:

Hence, the vertex, the maximum, is (3, 312.5), meaning that an increase of 3 times $1-price from the original $2 per bottle price maximizes the revenue. Thus, the price is $3 + $2 = $5
The y-intercept, is always at x = 0, and it is:
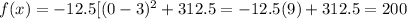
The x-intercepts are the solutions of the equation f(x) = 0.
You can find them easily by factoring the original equation:
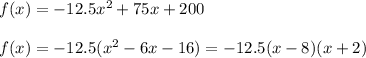
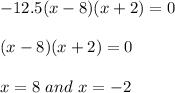
Thus, the x-intercepts occur at x = 8 and x = -2. Note that the vertex is at the symmetry axis, which is just in the middle between the two x-incercepsts:
-
- x = (8-2)/2 = 6/2 = 3, such as found above.
2. Model B.
Again, the vertex is at the symmetry axis, which is just in the middle between the two x-incercepsts.
In the graph you can see that the symmetry axis is the line x = 4:
- Midpoint between the two x-intercepts: x = (-2 + 10)/2 = 8/2 = 4.
Remenber, 4 is the number of $1 increases over the $ 2 per bottle price. Hence, for this model the price will be $4 + $2 = $6.
The y-intercept, the value of y when x = 0, is also read from the graph and it is between $ 180 and $ 210.