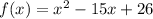Answer:
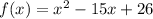
Explanation:
Assuming we want to write a quadratic function with intercepts x=13 and x=2.
Then we can work backwards.
This means that:
x-13=0 and x-2=0
The factored form of this quadratic function becomes:

We expand to get:
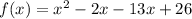
We simplify to obtain: