Question

Suppose the average mass of each of 20,000 asteroids in the solar system is 1017 kg. Compare the total mass of these asteroids to the mass of Earth. Assuming a spherical shape and a density of 3000 kg/m3, estimate the diameter of an asteroid having this average mass.

Answer 1

The mass of the asteroids is 0.000334896182184 times the mass of the Earth.

39929.4542466 m

Step-by-step explanation:

Total mass of the asteroids

`m_a20000* 10^(17)=2* 10^(21)\ kg`

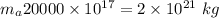
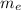`m_e` = Mass of Earth =
`5.972* 10^(24)\ kg`

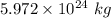
The ratio is

`(m_a)/(m_e)=(2* 10^(21))/(5.972* 10^(24))\\\Rightarrow (m_a)/(m_e)=0.000334896182184`

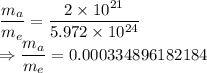
The mass of the asteroids is 0.000334896182184 times the mass of the Earth.

Volume is given by

`V=(m)/(\rho)\\\Rightarrow (4\pi)/(3* 8) d^3=(m)/(\rho)\\\Rightarrow d^3=(3* 8)/(4\pi)(m)/(\rho)\\\Rightarrow d=((3* 8)/(4\pi)(m)/(\rho))^{(1)/(3)}\\\Rightarrow d=((3* 8)/(4\pi)(10^(17))/(3000))^{(1)/(3)}\\\Rightarrow d=39929.4542466\ m`

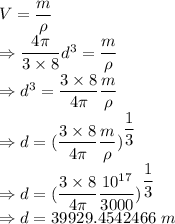
The diameter is 39929.4542466 m