The required 'option C) 144' is correct.
Explanation:
We have,
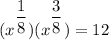
To find, the possible value of x = ?
∴
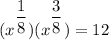
⇒
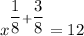
Using the exponential identity,

⇒
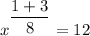
⇒
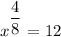
⇒
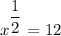
Squaring both sides, we get
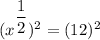
⇒

⇒ x = 144
∴ The possible value of x = 144
Thus, the required 'option C) 144' is correct.