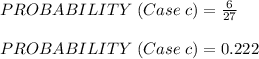Question

1) A family consisting of three persons—A, B, and C—goes to a medical clinic that always has a doctor at each of stations 1, 2, and 3. During a certain week, each member of the family visits the clinic once and is assigned at random to a station. The experiment consists of recording the station number for each member. Suppose that any incoming individual is equally likely to be assigned to any of the three stations irrespective of where other individuals have been assigned. What is the probability that

(a) All three family members are assigned to the same station? (Round your answer to three decimal places.)
(b) At most two family members are assigned to the same station? (Round your answer to three decimal places.)
(c) Every family member is assigned to a different station? (Round your answer to three decimal places.)

Answer 1

Explanation:

Let us record the station number 1, 2 or 3 for each family member A, B or C.

I am attaching a table containing total outcomes. Outcomes are presented along rows while the assigned station to each member is written along columns. For ease of understanding, 1 3 2 in the table should be interpreted as family member A being assigned to station 1, member B to station 3 and member C to station number 2, respectively.

From table it is clear that the total outcomes possible are 27.

We know that, probability can be defined as,

`PROBABITILY = (NUMBER\;OF\;DESIRED\;OUTCOMES)/(TOTAL\;NUMBER\;OF\;OUTCOMES)`

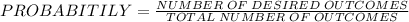
a) All Members Assigned to the Same Station.

Cases for all members being assigned to same station are as follows:

[1 1 1], [2 2 2], [3 3 3] (outcome number 1, 14 and 27 in the table).

Therefore,

`PROBABILITY\;(Case\;a) = (3)/(27)\\\\PROBABILITY\;(Case\;a) = 0.111`

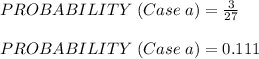
b) At Most Two Members Assigned to the Same Station.

It means that maximum of 2 members can have the same station. Cases for this situation are as follows:

[1 1 2], [1 1 3], [1 2 1], [1 2 2], [1 3 1], [1 3 3], [2 1 1], [2 1 2], [2 2 1], [2 2 3], [2 3 2],

[2 3 3], [3 1 1], [3 1 3], [3 2 2], [3 2 3], [3 3 1], [3 3 2]

(outcome number 2, 3, 4, 5, 7, 9, 10, 11, 13, 15, 17, 18, 19, 21, 23, 24, 25 and 26 in the table).

Therefore,

`PROBABILITY\;(Case\;b) = (18)/(27)\\\\PROBABILITY\;(Case\;b) = 0.666`

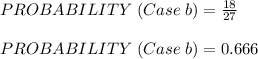
c) All Members Assigned to a Different Station.

For this scenario, we have the following results:

[1 2 3], [1 3 2], [2 1 3], [2 3 1], [3 1 2], [3 2 1] (outcome number 6, 8, 12, 16, 20 and 22 in the table).

Therefore,

`PROBABILITY\;(Case\;c) = (6)/(27)\\\\PROBABILITY\;(Case\;c) = 0.222`