Question

List the probability value for each possibility in the binomial experiment calculated at the beginning of this lab, which was calculated with the probability of a success being ½. (Complete sentence not necessary; round your answers to three decimal places)P(x=0) P(x=6)

P(x=1) P(x=7)
P(x=2) P(x=8)
P(x=3) P(x=9)
P(x=4) P(x=10)
P(x=5)

Answer 1

a. P(X = 0)= 0.001

b. P(X = 1)= 0.001

c. P(X=2)= 0.044

d. P(X=3)= 0.117

e. P(X=4)= 0.205

f. P(X=5)= 0.246

g. P(X=6)= 0.205

h. P(X=7)= 0.117

i. P(X=8)= 0.044

j. P(X=9)= 0.001

k. P(X=10)= 0.001

Explanation:

Hello!

You have the variable X with binomial distribution, the probability of success is 0.5 and the sample size is n= 10 (I suppose)

If the probability of success p=0.5 then the probability of failure is q= 1 - p= 1 - 0.5 ⇒ q= 0.5

You are asked to calculate the probabilities for each observed value of the variable. In this case is a discrete variable with definition between 0 and 10.

You have two ways of solving this excersice

1) Using the formula

`P(X)= (n!)/((n-X)!X!) * (p)^X * (q)^(n-X)`

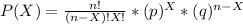
2) Using a table of cummulative probabilities of the binomial distribution.

a. P(X = 0)

Formula:

`P(X=0)= (10!)/((10-0)!0!) * (0.5)^0 * (0.5)^(10-0)`

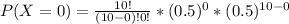
P(X = 0) = 0.00097 ≅ 0.001

Using the table:

P(X = 0) = P(X ≤ 0) = 0.0010

b. P(X = 1)

Formula

`P(X=1)= (10!)/((10-1)!1!) * (0.5)^1 * (0.5)^(10-1)`

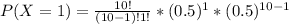
P(X = 1) = 0.0097 ≅ 0.001

Using table:

P(X = 1) = P(X ≤ 1) - P(X ≤ 0) = 0.0107-0.0010= 0.0097 ≅ 0.001

c. P(X=2)

Formula

`P(X=2)= (10!)/((10-2)!2!) * (0.5)^2 * (0.5)^(10-2)`

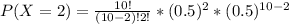
P(X = 2) = 0.0439 ≅ 0.044

Using table:

P(X = 2) = P(X ≤ 2) - P(X ≤ 1) = 0.0547 - 0.0107= 0.044

d. P(X = 3)

Formula

`P(X = 3)= (10!)/((10-3)!3!) * (0.5)^3 * (0.5)^(10-3)`

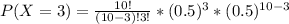
P(X = 3)= 0.11718 ≅ 0.1172

Using table:

P(X = 3) = P(X ≤ 3) - P(X ≤ 2) = 0.1719 - 0.0547= 0.1172

e. P(X = 4)

Formula

`P(X = 4)= (10!)/((10-4)!4!) * (0.5)^4 * (0.5)^(10-4)`

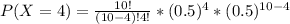
P(X = 4)= 0.2051

Using table:

P(X = 4) = P(X ≤ 4) - P(X ≤ 3) = 0.3770 - 0.1719= 0.2051

f. P(X = 5)

Formula

`P(X = 5)= (10!)/((10-5)!5!) * (0.5)^5 * (0.5)^(10-5)`

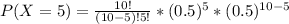
P(X = 5)= 0.2461 ≅ 0.246

Using table:

P(X = 5) = P(X ≤ 5) - P(X ≤ 4) = 0.6230 - 0.3770= 0.246

g. P(X = 6)

Formula

`P(X = 6)= (10!)/((10-6)!6!) * (0.5)^6 * (0.5)^(10-6)`

P(X = 6)= 0.2051

Using table:

P(X = 6) = P(X ≤ 6) - P(X ≤ 5) = 0.8281 - 0.6230 = 0.2051

h. P(X = 7)

Formula

`P(X = 7)= (10!)/((10-7)!7!) * (0.5)^7 * (0.5)^(10-7)`

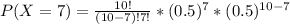
P(X = 7)= 0.11718 ≅ 0.1172

Using table:

P(X = 7) = P(X ≤ 7) - P(X ≤ 6) = 0.9453 - 0.8281= 0.1172

i. P(X = 8)

Formula

`P(X = 8)= (10!)/((10-8)!8!) * (0.5)^8 * (0.5)^(10-8)`

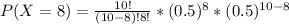
P(X = 8)= 0.0437 ≅ 0.044

Using table:

P(X = 8) = P(X ≤ 8) - P(X ≤ 7) = 0.9893 - 0.9453= 0.044

j. P(X = 9)

Formula

`P(X = 9)= (10!)/((10-9)!9!) * (0.5)^9 * (0.5)^(10-9)`

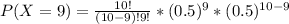
P(X = 9)=0.0097 ≅ 0.001

Using table:

P(X = 9) = P(X ≤ 9) - P(X ≤ 8) = 0.999 - 0.9893= 0.001

k. P(X = 10)

Formula

`P(X = 10)= (10!)/((10-10)!10!) * (0.5)^(10) * (0.5)^(10-10)`

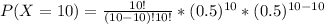
P(X = 10)= 0.00097 ≅ 0.001

Using table:

P(X = 10) = P(X ≤ 10) - P(X ≤ 9) = 1 - 0.9990= 0.001

Note: since 10 is the max number this variable can take, the cummulated probability until it is 1.

I hope it helps!