Question

Astronomers treat the number of stars in a given volume of space as a Poisson random variable. The density in the Milky Way Galaxy in the vicinity of our solar system is one star per 16 cubic light years.

How many cubic light years of space must be studied so that the probability of one or more stars exceeds 0.94?[Round your answer to the nearest integer.]

Answer 1

t = 45 cubic light years to find a star with this certainty.

Explanation:

The Poisson random probability equation is given by:

`P(k events in interval t)=((\lambda t)^(k)e^(-\lambda t))/(k!)`

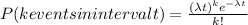
• λ is the density (1/16 star/cubic light years)
• t is the parameter in cubic light years

We can use the next equation to quantify how many cubic light years of space must be studied so that the probability of one or more stars exceeds 0.94.

`P(k\ge 1) \ge 0.94`

`1-f(0)=1-\frac{((1)/(16)*t)^(0)e^{-(1)/(16)*t}}{0!}=1-e^{-(1)/(16)*t}} \ge 0.94`

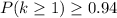
So, here we just need to solve it for t:

`1-e^{-(1)/(16)*t}} \ge 0.94`

`e^{-(1)/(16)*t}} \ge 0.06`

`ln(e^{-(1)/(16)*t}}) \ge ln(0.06)`

`-(1)/(16)*t \ge -2.8`

`t \ge 44.8`

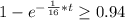
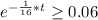
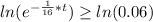
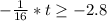
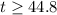
Therefore t = 45 cubic light years to find a star with this certainty.

I hope it helps you!