Question

Huck Finn walks at a speed of 0.70 m/sm/s across his raft (that is, he walks perpendicular to the raft's motion relative to the shore). The raft is traveling down the Mississippi River at a speed of 1.60 m/sm/s relative to the river bank. What is Huck's velocity (speed and direction) relative to the river bank?

Answer 1

Step-by-step explanation:

Given

Velocity of Huck w.r.t to raft
`v_(H,raft)=0.7\ m/s`

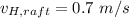
Perpendicular to the motion of raft

Velocity of Raft in the river
`v_(raft,river)=1.6\ m/s`

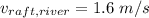
As Huck is traveling Perpendicular to the raft so he possess two velocities i.e. vertical velocity and horizontal velocity of River when observed from bank

`v_(Huck,river\ bank)=0.7\hat{j}+1.6\hat{i}`

So magnitude of velocity is given by

`|v|=√(0.7^2+1.6^2)`

`|v|=√(0.49+2.56)`

`|v|=√(3.05)`

`|v|=1.74\ m/s`

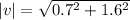
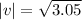
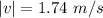
For direction
`\tan =(0.7)/(1.6)=0.4375`

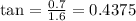
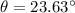`\theta =23.63^(\circ)` w.r.t river bank