Question

Beryllium-11 is a radioactive isotope of the alkaline metal Beryllium. It decays at a rate of 4.9% every second. Assuming you started with 100%, how much would be left after 45 seconds?\

Answer 1

11.02 % of an isotope will be left after 45 seconds.

Step-by-step explanation:

`N=N_o* e^(-\lambda t)\\\\\lambda =\frac{0.693}{t_{(1)/(2)}}`

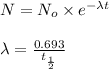
where,

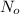`N_o` = initial mass of isotope

N = mass of the parent isotope left after the time, (t)

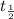`t_{(1)/(2)}` = half life of the isotope

`\lambda` = rate constant

We have :

Mass of Beryllium-11 radioactive isotope=
`N_o=100`

Mass of Beryllium-11 radioactive isotope after 45 seconds =
`N=?`

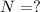
t = 45 s

`\lambda` = rate constant =
`4.9 \% s^(-1)=0.049 s^(-1)`

`N=N_o* e^(-(\lambda * t)`

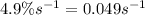
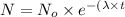
Now put all the given values in this formula, we get

`N=100* e^{-0.049 s^(-1)\ties 45 s}`

`N=11.02 g`

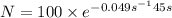
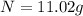
Percentage of isotope left :

`(N)/(N_o)* 100=(11.02 g)/(100 g)* 100=11.02\%`

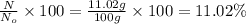
11.02 % of an isotope will be left after 45 seconds.