Question

Suppose that the distance, in miles, that people are willing to commute to work is an exponential random variable with a decay parameter \frac{1}{20}. Let X = the distance people are willing to commute in miles. What is m, μ, and σ? What is the probability that a person is willing to commute more than 25 miles?

Answer 1

• m =
  `(1)/(20)`
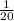
• μ = 20
• σ = 20

The probability that a person is willing to commute more than 25 miles is 0.2865.

Explanation:

Exponential probability distribution is used to define the probability distribution of the amount of time until some specific event takes place.

A random variable X follows an exponential distribution with parameter m.

The decay parameter is, m.

The probability distribution function of an Exponential distribution is:

`f(x)=me^(-mx)\ ;\ m>0, x>0`

Given: The decay parameter is,
`(1)/(20)`

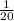
X is defined as the distance people are willing to commute in miles.

• The decay parameter is m =
  `(1)/(20)`.
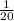• The mean of the distribution is:
  `\mu=(1)/(m)=(1)/((1)/(20))=20`.
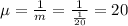• The standard deviation is:
  `\sigma=√(variance)= \sqrt{(1)/((m)^(2)) } =(1)/(m) =(1)/((1)/(20)) =20`

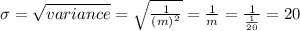
Compute the probability that a person is willing to commute more than 25 miles as follows:

`P(X>25)=\int\limits^(\infty)_(25) {(1)/(20) e^{-(1)/(20)x}} \, dx \\=(1)/(20)|20e^{-(1)/(20)x}|^(\infty)_(25)\\=|e^{-(1)/(20)x}|^(\infty)_(25)\\=e^{-(1)/(20)*25}\\=0.2865`

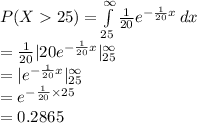
Thus, the probability that a person is willing to commute more than 25 miles is 0.2865.